단순 선형 회귀

이번 글에서는 단순 선형 회귀(univariate linear regression)에 대해서 알아봅니다.

목차

1. 모델의 표현

 - 표기법

 - 가설 함수

 - 단순 선형 회귀

2. 비용 함수

3. 경사 하강법

 - 경사 하강법이란

 - 선형 회귀를 위한 경사 하강법

 - 주의할 점

작성하면서 참고한 자료

Machine Learning, Andrew Ng

https://www.coursera.org/learn/machine-learning

기계 학습

---

모델의 표현

지난 글에서 다룬 집값의 예측 문제를 다시 생각해 봅니다. 이 문제는 각 데이터에 원하는 답인 '집값'의 정보가 포함되어 있기에 지도 학습(supervised learning) 문제였고, 집값이 연속적인 값이기 때문에 회귀(regression) 문제였습니다.

표기법

앞으로 사용할 표기법을 정하겠습니다. \(x^{(i)}\)는 특징(feature)이라고도 부르는 입력(input) 변수들이며, \(y^{(i)}\)는 타겟(target) 변수라고도 부르는 출력(output) 변수입니다. 집값 예측 문제에서 입력 변수들은 집의 면적 등이며 출력 변수는 집값이 됩니다. 순서쌍 \((x^{(i)},y^{(i)})\)는 훈련 예시(training example)라고 부르며, 학습에 사용되는 데이터셋(dataset) 전체를 훈련 세트(training set)라고 부르고 \((x^{(i)},y^{(i)});i=1,\cdots,m\)로 표기합니다. (\(m\)은 훈련 예시의 개수) 여기서 \({}^{(i)}\)로 표기하는 것은 그저 인덱스(index)를 나타낼 뿐 거듭제곱과는 관련이 없습니다. 마지막으로 \(X\)를 입력값들의 공간, \(Y\)를 출력값들의 공간이라고 합시다. 즉 집값 예측 문제에서 \(X=Y=\mathbb{R}\)입니다.

가설 함수

이제 지도 학습 문제에서 우리가 목표로 하는 것을 제대로 표기할 수 있습니다. 우리가 얻고 싶은 것은 입력값 \(x\)를 주었을 때 \(h(x)\)가 \(y\)를 잘 예측한 값이 되도록 하는 함수 \(h:X\to Y\)입니다. 훈련 세트를 학습 알고리즘을 통해 학습시켜 \(h\)를 얻고자 하는 것입니다. 이 함수 \(h\)는 역사적으로 가설 함수(hypothesis function)라고 불려왔습니다.

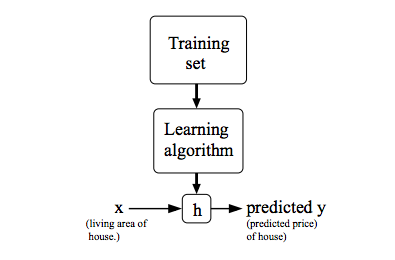
단순 선형 회귀

자, 그러면 어떻게 가설 함수 \(h\)를 표현할 수 있을까요? 우리는 가장 간단한 \(x\)에 대한 함수 중 하나가 일차함수인 것을 알고 있습니다. 즉, 다음과 같이 나타내도 괜찮을 것 같네요. \[h_\theta(x)=\theta_0+\theta_1x\] 이러한 모델을 변수가 하나인 선형 회귀(linear regression with one variable) 또는 단순 선형 회귀(univariate linear regression)라고 합니다. 또 \(\theta_0,\theta_1\)를 매개변수(parameters)라고 합니다. 앞으로의 논의에서 이 매개변수들의 값을 어떻게 선택할지에 집중하게 됩니다.

비용 함수

매개변수들의 값이 달라지면 가설 함수의 정확도 또한 달라집니다. 각 훈련 예시 \((x^{(i)},y^{(i)})\)에 대해 가설 함수의 오차는 \(h_\theta(x^{(i)})-y^{(i)}\)와 같은데, 오차의 절대값을 최소화하고 싶기 때문에 \[\sum^m_{i=1}(h_\theta(x^{(i)})-y^{(i)})^2\]와 같이 오차의 제곱의 합을 최소화하는 문제로 바꿀 수 있을 것입니다.

 

비용 함수(cost function)는 다음과 같이 정의합니다. \[J(\theta_0,\theta_1)=\frac{1}{2m}\sum^m_{i=1}(h_\theta(x^{(i)})-y^{(i)})^2\] 이것이 오차의 제곱의 평균을 2로 나눈 값이기 때문에, 평균 제곱 오차(mean squared error) 또는 제곱 오차 함수(squared error function)로도 불립니다. 앞서 살펴본 오차의 제곱의 합을 \(2m\)으로 나누어도 최소일 때의 매개변수 값들은 변하지 않습니다. \(m\)이 아니라 \(2m\)으로 나누는 이유는 뒤에 나오는 경사 하강법을 적용하여 비용 함수를 미분할 때 계산이 편해지기 때문입니다.

경사 하강법

경사 하강법이란

이제 비용 함수의 값을 최소화하는 문제를 풀기 위해 다음과 같은 경사 하강법(gradient descent)을 도입해 봅시다.

 

- 어떤 \(\theta_0,\theta_1\)으로 시작한다. (예를 들어, 둘 다 0)

- \(J(\theta_0,\theta_1)\)가 줄어드는 방향으로 \(\theta_0,\theta_1\)의 값을 바꾸어, 최소값에 도달할 때까지 계속한다.

 

\(J(\theta_0,\theta_1)\)가 줄어드는 방향을 알 수 있는 방법은 바로 미분입니다. \(\theta_0,\theta_1\) 각각에 대해 편미분을 하여 방향을 결정할 수 있습니다. 변화의 정도(크기)는 학습률(learning rate)이라고 불리는 \(\alpha\)값에 의해서 결정됩니다. 즉 새롭게 바뀌는 \(\theta_j\)는 다음의 식을 만족합니다. \[\theta_j:=\theta_j-\alpha\frac{\partial}{\partial\theta_j}J(\theta_0,\theta_1)\]

선형 회귀를 위한 경사 하강법

경사 하강법을 앞서 공부한 (단순) 선형 회귀 모델에 적용해 봅시다.

\[\begin{aligned}\theta_0-\alpha\frac{\partial }{\partial \theta_0}J(\theta_0,\theta_1)&=\theta_0-\alpha\frac{\partial }{\partial \theta_0}\frac{1}{2m}\sum^m_{i=1}(h_\theta(x^{(i)})-y^{(i)})^2\\&=\theta_0-\alpha\frac{1}{m}\sum^m_{i=1}(h_\theta(x^{(i)})-y^{(i)})\frac{\partial }{\partial \theta_0}(h_\theta(x^{(i)})-y^{(i)})\\&=\theta_0-\alpha\frac{1}{m}\sum^m_{i=1}(h_\theta(x^{(i)})-y^{(i)})\frac{\partial }{\partial \theta_0}(\theta_0+\theta_1x^{(i)}-y^{(i)})\\&=\theta_0-\alpha\frac{1}{m}\sum^m_{i=1}(h_\theta(x^{(i)})-y^{(i)})\end{aligned}\] \[\begin{aligned}\theta_1-\alpha\frac{\partial }{\partial \theta_1}J(\theta_0,\theta_1)&=\theta_1-\alpha\frac{\partial }{\partial \theta_1}\frac{1}{2m}\sum^m_{i=1}(h_\theta(x^{(i)})-y^{(i)})^2\\&=\theta_1-\alpha\frac{1}{m}\sum^m_{i=1}(h_\theta(x^{(i)})-y^{(i)})\frac{\partial }{\partial \theta_1}(h_\theta(x^{(i)})-y^{(i)})\\&=\theta_1-\alpha\frac{1}{m}\sum^m_{i=1}(h_\theta(x^{(i)})-y^{(i)})\frac{\partial }{\partial \theta_1}(\theta_0+\theta_1x^{(i)}-y^{(i)})\\&=\theta_1-\alpha\frac{1}{m}\sum^m_{i=1}((h_\theta(x^{(i)})-y^{(i)})x^{(i)})\end{aligned}\]

즉, 단순 선형 회귀를 위한 경사 하강법은 다음과 같습니다.

 

- 어떤 \(\theta_0,\theta_1\)으로 시작한다. (예를 들어, 둘 다 0)

- \(\theta_0:=\theta_0-\alpha\frac{1}{m}\sum^m_{i=1}(h_\theta(x^{(i)})-y^{(i)}),\quad\theta_1:=\theta_1-\alpha\frac{1}{m}\sum^m_{i=1}((h_\theta(x^{(i)})-y^{(i)})x^{(i)})\)가 되도록 \(\theta_0,\theta_1\)의 값을 바꾸어, 값이 변하지 않을 때까지 계속한다.

주의할 점

경사 하강법을 구현할 때 주의할 점이 있습니다. 매개변수의 값들을 모두 같은 시점에 바꾸어야 합니다. 만약 \(\theta_0,\theta_1\)을 따로따로 바꾼다면, \(J(\theta_0,\theta_1)\)가 중간에 바뀌어버려 원하지 않는 매개변수값을 얻게 됩니다. 그래서 임시 변수(temporary variable)를 사용해서 바뀔 매개변수의 값들을 저장해야 합니다.

 

경사 하강법을 통해 얻는 매개 변수의 값들이 반드시 \(J\)의 최소값을 보장하는 것은 아닙니다. \(J\)가 반드시 극소값이기는 하지만, 최소값인지는 알 수 없습니다. 다만, 단순 선형 회귀에서는 \(J\)가 극소일 경우 반드시 그것이 최소가 됨이 알려져 있습니다.

 

지금까지 알아본 경사 하강법은 각 단계에서 모든 훈련 예시를 보기 때문에, 배치 경사 하강법(batch gradient descent)이라고 부릅니다.

---

다음 글에서는 다변수 선형 회귀에 대해 알아보겠습니다.